T-Test vs Z-Test: Breaking Down the Examples and Differences
Statistics can be a daunting subject, but it’s crucial to understand the various tests that are used to analyze data. Two of the most commonly used statistical tests are T-test and Z-test. While they may seem similar at first glance, there are key differences between them that can make all the difference in your analysis. In this blog post, we’ll break down everything you need to know about T-Test vs Z-Test and help you determine which test is best suited for your data analysis needs!
T-Test Vs Z-Test (Comparison Chart)
| T-test | Z-test |
|---|---|
| A T-test refers to a statistical test used by researchers to determine the significant difference between the means of two groups when population standard deviation is not given. | A Z-test refers to a statistical test used by researchers to measure/determine if there is a significant difference between two given population means. It is typically used when the sample size is large or when the population standard deviation is known. |
| T-test uses t-statistic to calculate the p-value. | It uses Z-score to calculate the p-value. |
| The T-test is used with a small sample size (n<30). | Z-test is used with the recommended large sample size (n > 30). |
| T-test is comparatively more flexible in terms of analysis and design than Z-test. | Z-test is less flexible in terms of analysis as it depends on population parameters. |
| It might be less powerful in detecting small differences. | It can be more powerful in detecting small differences. |
| T-test assumes the data follows a student’s t-distribution. | The Z-test assumes the data follows a standard normal distribution. |
| T-test is commonly used in situations where the sample size is small and the population standard deviation is unknown. | Z-test is commonly used when the sample size is large and the population standard deviation is known or assumed. |
| For Example, Comparing the mean heights of two groups of students where the sample sizes are small and the population standard deviation is unknown. | For Example, testing the mean weight of the population against a known value where the sample size is large and the population standard deviation is known. |
What is T-Test?
A T-test is a type of statistical test used to compare the means of two independent or unrelated samples. It is commonly used to determine whether two groups are statistically different from each other. This test uses the t-statistic, which measures the difference between two groups when the population standard deviation is not given. The T-test is also known as the Student’s T-test because it was developed by William Gosset under the pseudonym “Student”.
The three basic assumptions of the t-test are:
- The samples are independent of each other
- The size of the sample is small (n<30)
- Sample values should be recorded accurately.
T-test can be calculated as:

Where:
t is the t-value
X̄ is the sample mean
μ is the population mean
s is the sample standard deviation
n is the sample size.
Pros of T-test
- Suitable for Small Sample Size – The t-test is a good choice when the sample size is small. This makes it especially suitable for situations where the population size is too large to study.
- Flexibility – The t-test can be used with different types of data, including categorical and ordinal. Additionally, it can also be used in cases where parametric assumptions have not been met.
- Easy to Understand: The t-test is easy to understand and interpret, making it an attractive option for researchers without advanced statistical knowledge.
- Allows for Unequal Variances – The t-test is robust to unequal variances, meaning that it can handle data sets with unequal sample sizes and different variances.
Cons of T-test
- Assumptions – The t-test requires certain assumptions to be made about the data, such as normality and homoscedasticity (equal variances). If these conditions are violated, then the results may not be valid.
- Limited Information – The t-test provides limited information on the data set as it only compares two means at a time. Therefore, other tests such as ANOVA may need to be used in order to gain further insight into the data set.
- Limited Power – The t-test has limited power when compared to other statistical tests, such as ANOVA or multiple regression. This means that there may be cases where it is not capable of detecting significant differences between two groups.
What is Z-Test
A Z-test is a type of statistical test used to assess the differences between population means when the standard deviation is known and when the sample size is large (n>30). It compares the difference between two sample means (or proportions) to a standard normal distribution and provides a measure of confidence in that difference. Unlike a T-test, which requires only two samples, a Z-test can be used with multiple samples.
The three basic assumptions of Z -test are:
- The population of observations is normally distributed
- A sample size (n) should be sufficiently large (n>30)
- The standard deviation of the population is known.
Z-test Can be calculated as:
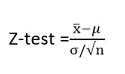
Where:
z is the z-value
X̄ is the sample mean
μ is the population mean (known)
σ is the population standard deviation (known)
n is the sample size.
Pros of Z-test
- Suitable for Large Sample Size – Z-test is one of the most widely used statistical tests because it can be applied to large sample sizes. This makes it ideal for testing hypotheses involving large datasets.
- Relatively Easy to Understand and Use – Unlike other tests, Z-test does not require complex calculations and is relatively easy to interpret. It is a great choice for students who are just beginning to learn statistics.
- Highly precise – Due to its reliance on larger sample sizes, z-test results are highly accurate and precise. This makes it an excellent choice when looking for reliable results with minimal variance.
Cons of Z-test
- Not suitable for small sample size – Because the z-test relies on larger sample sizes, it is not suitable for testing hypotheses involving smaller datasets. As such, other tests such as t-tests should be used instead in these cases.
- Can be difficult to interpret – The output of a z-test includes many values which can make it difficult to interpret the results accurately without prior knowledge or experience in statistics.
Key Differences Between T-test and Z-test
While comparing t-test vs z-test, here we have included some of the key differences between them.
- Population Standard Deviation – The t-test is used when the population standard deviation is unknown, while the z-test is used when the population standard deviation is known.
- P-Value Calculation – The t-statistic is used to calculate the p-value in a t-test, while the z-score is used to calculate the p-value in a z-test.
- Sensitivity to Outliers – the t-test is more sensitive to outliers than the z-test.
- Flexibility, the t-test is more flexible than the z-test in terms of design and analysis.

Example of T-Test
A researcher wants to investigate the impact of a new educational program on student performance. The researcher randomly assigns students from an elementary school into two groups: Group A and Group B. Group A receives the new educational program while Group B continues with the traditional program. After one year, the researcher gathers data on student performance for both groups and performs a T-test to determine if there is a statistically significant difference between the two groups.
The results of the T-test indicate that there is a statistically significant difference between the two groups, with Group A showing higher performance than Group B. This suggests that the new educational program had a positive effect on student performance.
Examples of Z-Test
- A pharmaceutical company wants to compare the effectiveness of two different drugs in lowering blood pressure. The company randomly assigns 100 participants to either Drug A or Drug B and then measures their blood pressure after six weeks. A z-test can be used to determine if there is a statistically significant difference between the two groups in terms of the average reduction in blood pressure.
- A researcher wants to know if there is a difference in the average test scores of students who attend private schools versus those who attend public schools. He collects data from 100 students from each type of school and calculates the mean test score for each group. He can use a z-test to determine if there is a statistically significant difference between the two groups’ average test scores.
When Should I Use a T or Z Test?
There are a few key instances in which you would want to use a T or Z test. If you have a large enough sample size (n > 30), then you can use either test, but if your sample size is small (n < 30), then you must use a T-test. Additionally, if your data is Normally distributed, you can use either test, but if your data is not Normally distributed, you must use a T-test.
Another key factor to consider is whether or not you know the population standard deviation. If you do know the population standard deviation, then you can use a Z-test. If you do not know the population standard deviation (or can only estimate it), then you must use a T-test.
Here is a quick summary of when to use each type of test:
– Use a T-test when your sample size is small or when the distribution of your data is not Normal.
– Use a Z test when your sample size is large and the distribution of your data is Normal.
Conclusion
Understanding the differences between a T-test and a Z-test is important for any researcher. Both tests measure the mean of two populations, but they differ in their assumptions about population variance, sample size, and effect size. While the T-test can be used with small samples or when data is not normally distributed, the Z-Test should only be used with large samples and normally distributed data. Knowing which test to use can help you make more informed decisions in your research projects.



